

Would you call the above image a photograph? In one sense, it meets the standard criteria - its production began with the focusing of light upon a light-sensitive material.
Yet, the infrared light that produced this image is not visible to the human eye. In order for you to see it, the camera manufacturer had to map this information to a visible portion of the electromagnetic spectrum. In this case, a range of infrared intensity was mapped to a range of green intensity. The camera manufacturer could have chosen a different mapping. The choice may not be entirely arbitrary, but it is indeed a mapping, a translation of media.
Therefore, our experience of the above image arguably has more in common with the experience of a weather map than with a conventional photograph.
This leads to the somewhat unsettling notion that, in a sense, human vision is itself a kind of data visualization.
Our eyes send electrical signals that correspond to something real - the physical interaction of light with our surrounding environment. But the way that we perceive these signals has a fundamental similarity to the sorts of data visualizations described above. They are mappings from one kind of information to another.
Q: Does the world really look like what we see?
A: It does to us.
Q: But what does the world really look like?
A: This question implies a perceiver. If the question were "what does the world look like to no one?" then the answer should presumably be "nothing!" But, that does not mean that the world doesn't exist. It just means that the world exists in its own medium, which is not identical to the medium in which we perceive it.
In philosophical terms, this idea stems back to Immanuel Kant's distinction between noumena or things as they are in themselves and phenomena or things as they appear to us.
As we begin our study of machine learning, it is important to recognize that perception can never be fully synonymous with any underlying objective reality. The perceiver's reality is the product of experience, which is inherently finite and incomplete. So, while the output of a machine learning system may be correct with respect to its own experience, it cannot be universal or objective. This means that a machine learning system cannot, for example, objectively classify human facial expressions. It can only do so with respect to the non-objective mappings it has learned from a specific dataset.
In our everyday communication, we generally use what logicians call fuzzy logic. This form of logic relates to approximate rather than exact reasoning. For example, we might identify an object as being:

These statements do not hold an exact meaning and are often context-dependent. When we say that a car is small, this implies a very different scale than when we say that a planet is small.

Describing an object in these terms requires an auxiliary knowledge of the range of possible values that exists within a specific domain of meaning.

If we had only seen one car ever, we would not be able to distinguish a small car from a large one.
Even if we had seen a handful of cars, we could not say with great assurance that we knew the full range of possible car sizes.
With sufficient experience, we could never be completely sure that we had seen the smallest and largest of all cars. But we could feel relatively certain that we had a good approximation of the range.
Since the people around us will tend to have had relatively similar experiences of cars, we can meaningfully discuss them with one another in fuzzy terms.
Computers, however, have not traditionally had access to this sort of auxiliary knowledge. Instead, they have lived a life of experiential deprivation.

As such, traditional computing platforms have been designed to operate on logical expressions that can be evaluated without the knowledge of any outside factor beyond those expressly provided to them.
Though fuzzy logical expressions can be employed by traditional platforms through the programmer’s or user’s explicit delineation of a fuzzy term such as very small, these systems have generally been designed to deal with boolean logic (also called binary logic), in which every expression must ultimately evaluate to either true or false.
One rationale for this approach is that boolean logic allows a computer program’s behavior to be defined as a finite set of concrete states, making it easier to build and test systems that will behave in a predictable manner and conform precisely to their programmer’s intentions.
Machine learning changes all of this by providing mechanisms for imparting experiential knowledge upon computing systems.
These technologies enable machines to deal with fuzzier and more complex or human concepts, but also bring an assortment of design challenges related to the sometimes problematic nature of working with imprecise terminology and unpredictable behavior.
Additional Resources
A traditional computer program is a lot like a choose-your-own-adventure book, which contains instructions to the reader such as: “If you want the prince to fight the dragon, turn to page 32.”
In code, we use conditionals (also called if-statements) to move the user to a particular portion of the code when a set of pre-defined conditions have been met. For example:
if( mouse button is pressed and mouse is over 'Login' button )
show 'Welcome' screen;Using this mechanism, we can define each of a program’s possible states and the exact conditions under which the user will be able to transition between them. As a result, the program’s overall behavior should be predictable, repeatable and testable.
It is possible that a programmer might overlook some particular condition and introduce a bug as a result:
if( grade is greater than 65 )
return 'Pass';
else if( grade is less than 65 )
return 'Fail';
// What happens if grade is equal to 65?But, it is at least conceptually possible to methodically probe every possible path within the choose-your-own-adventure and plug any holes that may exist in the program’s logic.
The behavior of machine learning systems, on the other hand, is not defined through this kind of explicit programming process. Rather than using an explicit set of rules to describe a program’s possible behaviors, a machine learning system approximates a set of rules from a set of example behaviors. This is somewhat like our own mental processes for learning about the world around us.
Long before we encounter any formal description of the laws of physics, we learn to operate within them by observing the outcomes of our interactions with the physical world.

A child may have no awareness of Newton’s equations, but through repeated observation and experimentation, the child will come to recognize patterns in the relationships between the physical properties and behaviors of objects.
In the context of human intelligence, we often call this intuition. Intuition provides an extremely effective mechanism for operating on complex systems. But it does not yield an explicit set of rules that can be easily inspected or fine-tuned.
In a machine learning system, these intuitions are encoded as a set of numerical values. A visualization of these values might look something like this:

It is virtually impossible to look at these values and get a sense of how the system will behave in response to a particular set of conditions. To test the system, we need to run example inputs through it. But, there is no guarantee that these tests will address all aspects of the system’s behaviors. To fine-tune the system’s behaviors in relation to a particular set of conditions, all we can do is alter the set of examples we use to train the system.
Machine learning systems generally require a very large number of examples to produce a strong intuition for a complex set of behaviors. To extrapolate a good approximation of the rules, the learner must observe many variations of their application. The learner must be exposed to the more extreme or unlikely behaviors of a system as well as the most likely ones.
While intuitive learners may be slower at rote procedural tasks such as those performed by a calculator, they are able to perform much more complex tasks that do not lend themselves to exact procedures.
But, even with an immense amount of training, these intuitive approaches sometimes fail us.

We sometimes mistakenly identify a human face in a grilled cheese sandwich, for example.
A key principle in the design of conventional programming languages is that each feature should work in a predictable, repeatable manner provided that the feature is being used correctly by the programmer.
No matter how many times we perform an arithmetic operation such as “2 + 2,” we should always get the same answer. If this is ever not the case, then a bug exists in the language or tool we are using. Though it is not inconceivable for a programming language to contain a bug, it is relatively rare and would almost never relate to such a commonly used operator.
To be extra certain that conventional code will operate as expected, most large codebases employ a set of formal unit tests to ensure that the functionality of the system is fully in line with the developer’s expectations.

So, bugs aside, conventional programming languages can be seen as systems that are always correct about mundane things like concrete mathematical operations.
Machine learning algorithms, on the other hand, can be thought of as systems that are often correct about more complicated things like identifying human faces in an image.
A machine learning system is designed to approximate a set of demonstrated behaviors. This precludes it from behaving in an entirely predictable and reproducible manner, even if it has been properly trained on an extremely large number of examples.
This is not to say, of course, that a well-trained machine learning system’s behavior must be erratic. Rather, it should be understood and considered within the design of machine-learning-enhanced systems that their capacity for dealing with extraordinarily complex concepts and patterns also comes with a certain degree of imprecision and unpredictability beyond what can be expected from traditional computing platforms.
In logic, there are two main ways of reasoning about how a set of rules and observations relate to one another.
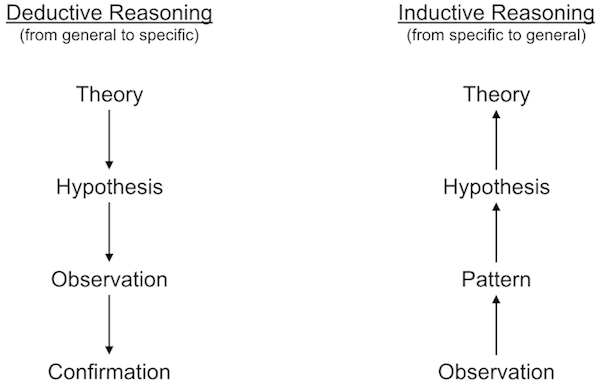
In some cases, we have a general sense of the principles that govern a system, but need to confirm that our beliefs hold true across many specific instances. This is called deductive reasoning.
In deductive reasoning, we start with a broad theory about the rules of a system, distill this theory into more specific hypotheses, gather observations and test those observations against our hypotheses in order to confirm whether the original theory was correct.
In other cases, we have made a set of observations and wish to develop a general theory that explains them. This is called inductive reasoning.
In inductive reasoning, we start with a group of specific observations, look for patterns in those observations and formulate tentative hypotheses in order to produce a general theory that encompasses our original observations.
Machine learning systems can be seen as tools that assist or automate inductive reasoning processes.
In other words, we provide them with a set of examples and they try to discover the underlying correlations or rules expressed by those examples.
This is a powerful thing because it means that machines can help us to see the big picture and find patterns in very complicated phenomena.
The video below of Richard Feynman discussing the process of observing the rules of chess offers a nice analogy for understanding inductive reasoning:
From Richard Feynman - The Pleasure of Finding Things Out
Let's look at a few puzzles that evoke our own inductive powers and then think about how a machine performs induction.
In a simple system that has a small number of rules, it is often quite easy to produce a general theory from a handful of examples. Consider the following:
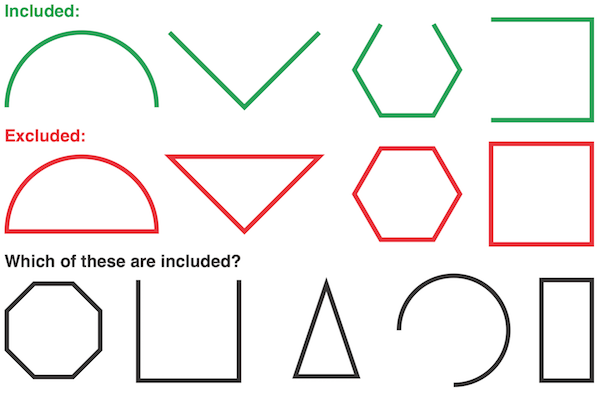
In this system, you should have no trouble uncovering the singular rule that governs inclusion: open figures are included and closed figures are excluded. Once discovered, you can easily apply this rule to the uncategorized figures in the bottom row.
In this next example, you may have to look a bit harder:
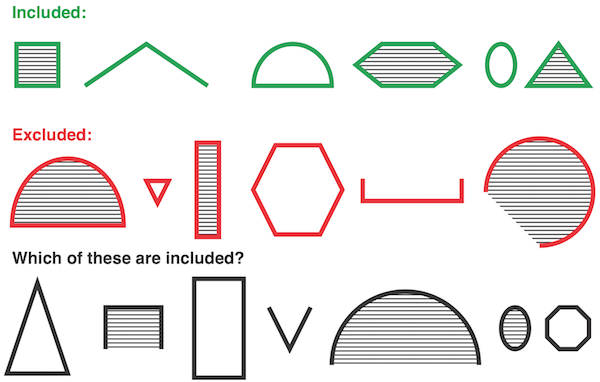
Here, there seem to be more variables involved.
You may have considered the shape and shading of each figure before discovering that in fact this system is also governed by a single attribute: the figure’s height. If it took you a moment to discover the rule, it is likely because you spent time considering attributes that seemed important but were ultimately not. This kind of noise exists in many systems, making it more difficult to isolate the meaningful attributes.
To get a better sense of how machine learning algorithms actually perform induction, let’s consider this next example:
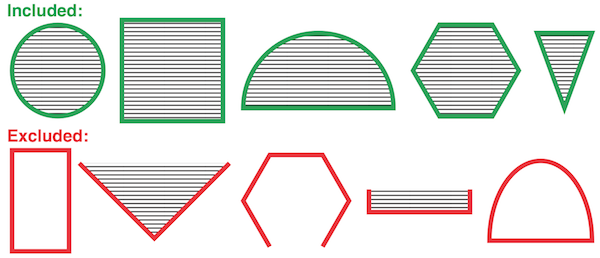
This system is equivalent to the boolean logical expression, AND. In other words, only figures that are both shaded and closed are included.
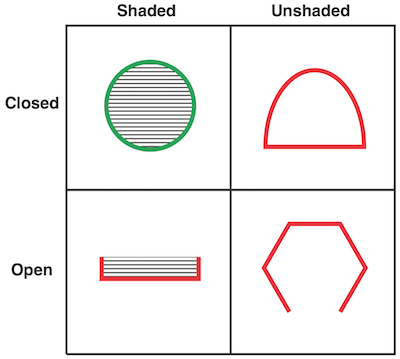
Before we look at induction, let’s first consider how we would implement this logic in an electrical system from a deductive point of view. In other words, if we already knew the rule, how could we implement it in an electrical device?
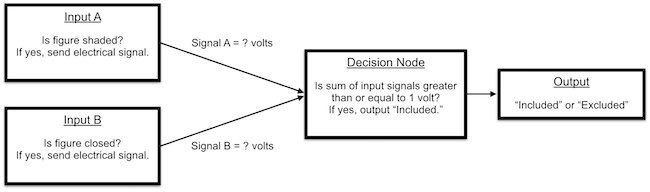
In the above diagram, we have a wire leading from each input attribute to a decision node.
If a figure is shaded, then an electrical signal will be sent through the wire leading from Input A. If the figure is closed, then an electrical signal will be sent through the wire leading from Input B.
The decision node will output an electrical signal indicating that the figure is included if the sum of its input signals is greater than or equal to 1 volt.
To implement the AND gate, we need to set the voltage associated with each of the two input signals.
Since the output threshold is 1 volt and we only want the output to be triggered if both inputs are active, we can set the voltage associated with each input to a half volt. If only one or neither input is active, the output threshold will not be reached. We could now use this electronic device to deduce the correct output for any example input.
Now, let’s consider the same problem from an inductive point of view.
In this case, we have a set of example inputs and outputs that exemplify a rule but do not know what the rule is. We will try to determine the nature of the rule using these examples. Let’s again assume that the decision node’s output threshold is 1 volt.
To reproduce the behavior of the AND gate by induction, we need to find voltage levels for the input signals that will produce the expected output for each pair of example inputs.
The process of discovering the right combination of voltages can be seen as a kind of search problem.
One approach we could take is to choose random voltages for the input signals, use these to predict the output of each example and compare these predictions to the correct outputs.
If the predictions match the correct outputs, then we have found good voltage levels. If not, we could choose new random voltages and start the process over. This process of choosing random voltages could be repeated until the system consistently predicted the correct output for each example.
In a simple system like this one, a guess-and-check approach may allow us to arrive at suitable values within a reasonable amount of time. But for a system that involves many more attributes, the number of possible combinations of signal voltages would be immense and we would be unlikely to guess suitable values efficiently. With each additional attribute, we would need to search for a needle in an increasingly large haystack.
Rather than guessing randomly and starting over when the results are not suitable, we could instead take an iterative approach. We could start with random values and check the output predictions they yield. Rather than starting over if the results are inaccurate, we could instead look at the extent and direction of that inaccuracy and try to incrementally adjust the voltages to produce more accurate results.
This process is a simplified version of the learning procedure used by one of the earliest machine learning systems, called a Perceptron. Perceptrons are capable of performing inductive learning on simple systems, but they are not capable of solving more complex learning problems. Nonetheless, the Perceptron learning procedure gives a taste of how machine learning systems perform induction.
In machine learning, the terms supervised, unsupervised, semi-supervised, and reinforcement learning are used to describe some of the key differences in how various models and algorithms learn and what they learn about. There are many additional terms used within the field of machine learning to describe other important distinctions, but these four categories provide a basic vocabulary for discussing the main types of machine learning systems.

Supervised learning procedures are used in problems for which we can provide the system with example inputs as well as their corresponding outputs and wish to induce an implicit approximation of the rules or function that governs these correlations.
Procedures of this kind are supervised in the sense that we explicitly indicate what correlations should be found and only ask the machine how to substantiate these correlations. Once trained, a supervised learning system should be able to predict the correct output for an input example that is similar in nature to the training set, but not explicitly contained within it.
The kinds of problems that can be addressed by supervised learning procedures are generally divided into two categories: classification and regression problems.
In a classification problem, the outputs relate to a set of discrete categories. For example, we may have an image of a handwritten character and wish to determine which of 26 possible letters it represents.
In a regression problem, the outputs relate to a real-valued number. For example, based on a set of financial metrics and past performance data, we may try to guess the future price of a particular stock.

Unsupervised learning procedures do not require a set of known outputs. Instead, the machine is tasked with finding internal patterns within the training examples. Procedures of this kind are unsupervised in the sense that we do not explicitly indicate what the system should learn about.
Instead, we provide a set of training examples that we believe contains internal patterns and leave it to the system to discover those patterns on its own.
In general, unsupervised learning can provide assistance in our efforts to understand extremely complex systems whose internal patterns may be too complex for humans to discover on their own.
Unsupervised learning can also be used to produce generative models, which can, for example, learn the stylistic patterns in a particular composer’s work and then generate new compositions in that style.
Unsupervised learning has been a subject of increasing excitement and plays a key role in the deep learning renaissance. One of the main causes of this excitement has been the realization that unsupervised learning can be used to dramatically improve the quality of supervised learning processes.

Semi-supervised learning procedures use the automatic feature discovery capabilities of unsupervised learning systems to improve the quality of predictions in a supervised learning problem.
Instead of trying to correlate raw input data with the known outputs, the raw inputs are first interpreted by an unsupervised system. The unsupervised system tries to discover internal patterns within the raw input data, removing some of the noise and helping to bring forward the most important or indicative features of the data.
These distilled versions of the data are then handed over to a supervised learning model, which correlates the distilled inputs with their corresponding outputs in order to produce a predictive model whose accuracy is generally far greater than that of a purely supervised learning system.
This approach can be particularly useful in cases where only a small portion of the available training examples have been associated with a known output. One such example is the task of correlating photographic images with the names of the objects they depict.
An immense number of photographic images can be found on the Web, but only a small percentage of them come with reliable linguistic associations. Semi-supervised learning allows the system to discover internal patterns within the full set of images and associate these patterns with the descriptive labels that were provided for a limited number of examples.
This approach bears some resemblance to our own learning process in the sense that we have many experiences interacting with a particular kind of object, but a much smaller number of experiences in which another person explicitly tells us the name of that object.

Reinforcement learning procedures use rewards and punishments to shape the behavior of a system with respect to one or several specific goals.
Unlike supervised and unsupervised learning systems, reinforcement learning systems are not generally trained on an existent dataset and instead learn primarily from the feedback they gather through performing actions and observing the consequences.
In systems of this kind, the machine is tasked with discovering behaviors that result in the greatest reward, an approach which is particularly applicable to robotics and tasks like learning to play a board game in which it is possible to explicitly define the characteristics of a successful action but not how and when to perform those actions in all possible scenarios.
Being able to produce the correct output for a given input is not necessarily a sign of learning or intelligence. It is important to consider how the output was achieved. It is not always easy to tell the difference between a rote operation and an intelligent one.
The items shown below can be described by concrete, general-purpose formulae and therefore can be performed by a machine without any learning.
It is also possible for a machine to learn these operations. But, when a concrete formula exists, it is almost always more efficient to use it over a learned approach. Learning is computationally intensive and should therefore be reserved for tasks that are not easily described by a concrete formula.
Arithmetic Operators
Logical Truth Tables
| P | Q | P and Q | P or Q | P exclusive-or Q |
|---|---|---|---|---|
| T | T | T | T | F |
| T | F | F | T | T |
| F | T | F | T | T |
| F | F | F | F | F |
Lookup Tables
| X | sqrt( X ) |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
Encoding Schemes
Hello, World
print "Hello, World!"Variables
myInt = 2
myReal = 3.14
myString = "hello"
print myInt
print myReal
print myStringArithmetic Operators
print ( 1 + 2 )
print ( 3 - 1 )
print ( 2 * 3.14 )
print ( 8 / 3 )
print ( 8 / 3.0 )String Operators
myString = "hello"
print( len( myString ) ) # prints string length
print( myString[0] ) # prints "h"
print( myString[0:2] ) # prints "he"
myString = myString.upper() # converts string to uppercase
myString = myString.lower() # converts string to lowercase
if "hello" == "hello":
print( "'hello' is equal to 'hello'" )
if "hello" in "hello world":
print( "'hello world' contains 'hello'" )Lists
myList = [ "alfa", "bravo", "charlie", "delta", "echo" ]
print myList # prints all elements
print myList[ 0 ] # prints first element
print myList[ 1 ] # prints second element
myList.append( "foxtrot" ) # adds element
myList.remove( "charlie" ) # removes element
myList.sort() # sorts the list in alphabetical order
myList.reverse() # reverses orderLoops
for i in range( 1, 10 ):
print i
myList = [ "alfa", "bravo", "charlie", "delta", "echo" ]
for item in myList:
print itemConditionals
x = 7
if x < 10:
print 'x is less than 10'
else:
print 'x is greater than or equal to 10'
if x > 10 and x < 20:
print "x is in range"
else:
print "x is out of range"Functions
def myFunc(x):
return x*x
print myFunc( 3 )Assignment
Readings
Optional